If you are going to use Javascript for the coding interview, be prepared for heaps
Javascript is great. It’s simple.
It’s dynamically typed. There isn’t too much “boiler plate” code, unlike Java.
It’s a solid choice for a coding interview.
But there is one thing that Javascript falls short of other popular languages that can make you perform bad in interviews.
Javascript does not have a standard heap / priority queue data structure that you can use out of the box.
Imagine you get a question where the optimal runtime and space complexity is only achievable by using a priority queue / heap. What do you do?
Sure, there are npm libraries out there done by individuals, but are you really going to import npm modules during your interview? If your interviewer is cool with it, maybe. But unless it’s a well-known package like Lodash, it could be frowned upon.
Other languages like Python and Java have these data structures built into their libraries, but Javascript falls short on this one.
So let’s talk about what you should do with Javascript when an interviewer asks a heap question.
Intro
Q: What kind of heaps are we talking about?
In this post, we are talking about Binary Heaps. If you don’t know what they are, read this
Q: What kind of ordering of Binary Heaps are we talking about?
We are talking about min-heap and max-heap orderings.
Min-heap: value of the node is less than its children.
Max-heap: value of the node is greater than its children.
“Heap is not necessary to solve a question”
True.
You can still solve a question without using a heap.
But there are questions where using a heap will get you the optimal runtime and space complexity, which is why there is such an advantage to using it.
Here’s an example question, taken from Leetcode.
Question 1
Kth Smallest Element in a Sorted Matrix
Given a n x n matrix where each of the rows and columns are sorted in ascending order, find the kth smallest element in the matrix.
Note that it is the kth smallest element in the sorted order, not the kth distinct element.
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
return 13.If you haven’t solved this question, try solving it before reading the solution!!
Solution without heaps
You could simply solve this by putting all the elements into an array, sorting it and returning the element at the kth index.
Sorted Array: [1,5,9,10,11,12,13,13,15]
Index to return: array.length - k
Problem solved.
But what is your space and runtime complexity?
Runtime
Quicksort: O( nlog(n) ) average, O( n^2 ) worst case
Accessing k-th index: O( 1 )
Total: O( nlog(n) ) average, O( n^2 ) worst case
Space
Quicksort: O( log(n) ) average
Constructing the final sorted array: O( n )
Total: O( n )
Why Quicksort? Because that’s what the Javascript V8 Engine (the stuff that runs on Google Chrome, Node, etc) uses. You can read more about it here.
Also you need to know this: even though Quicksort sorts everything in-place, it partitions the array and calls itself recursively, which adds to the space (stack) complexity.
Solution using heaps
Now, let’s compare against the heap solution. What are the runtimes & space if you were to use a heap?
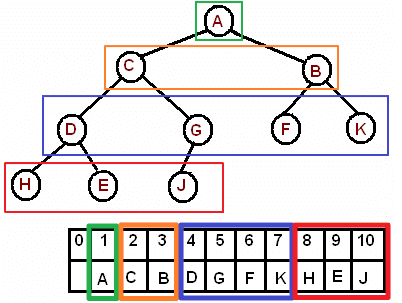
Since we are using Javascript, we need to use an array-implementation of a heap. The following picture helps you get an idea.
This is not your normal heap you use in Python. It’s an array-based workaround of a heap in Javascript, because heap data structures don’t exist in Javascript. In my solutions, I’m assuming I get to use the minHeapify() function I defined at the end of this post
With this, you could solve the problem within the following runtime and space complexities:
Runtime:
Array-based heapify function: O( log(n) )
Heapify O( log(n) ) each element in the array O( n ): O( n * log(n) )
Remove k - 1 elements, and heapify each time: O( k * log(n) )
Total: O( nlog(n) )
You could achieve a lower runtime of O( nlog(k) ) if you were to perhaps implement the heap with a max_size and polling functionality, but I didn’t do that. I didn’t think I would get enough time in an interview to write all that, on top of solving my actual question. I wanted to keep things simple and went with a function I defined below. Always communicate with your interviewer about stuff like this, maybe they will even allow you to assume the function already exists and can be used without defining it.
Space
Constructing the initial un-heapified array: O( n )
Heapify in-place: O( 1 )
Total: O( n )
The following table summarizies the comparison.
| Runtime | Space | |
|---|---|---|
| No heap | O( nlog(n) ) average O( n^2 ) worst case |
O( n ) |
| Heap | O( nlog(n) ) | O( n ) |
You might be asking, what’s the point of using a heap if you get the same average runtime?
Fair question. For this question, there isn’t a strong incentive besides avoiding that worst-case runtime of O( n^2 ). I will illustrate the benefit of this method in the next question. I just wanted to show the usage of array-based heap implementation first.
But for your general knowledge, note that to heapify an array, you only require constant space, as long as you implement iteratively. You can find an example of iterative implementation in Javascript further down this post, or here in Java (just so you get the idea).
Anyways, you might be thinking “This is not very useful”. Let’s move on to a question where the difference is substantial.
Question 2
Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.
Input:
[
1->4->5,
1->3->4,
2->6
]Output: 1->1->2->3->4->4->5->6
If you haven’t solved this question, try solving it before reading the solution!!
Solution without heaps
Without using a heap, you could solve this question by sorting each array by their first element, in ascending order.
Then you pop the first element from the first array and add it to your output.
You do this each time you pop an element and add it to your output.
Runtime
There are k arrays and n elements.
Sorting k arrays by their first element will take O( klog(k)) time on average. O( k^2 ) worst case.
You are doing this for each n elements. Worst-case scenario would be where all k arrays had an equal amount of elements. Best-case would be where there’s only 1 array with n elements.
So your total runtime will be O( nklog(k) ) average, O( nk^2 ) worst case, O( n ) best case (just one array).
Space
Additional space complexity will be coming from the Quicksort: O( log(k) ).
Solution using heaps
What if you use a heap?
We are assuming to use an array-based Javascript implementation of a heap, not a normal Python heap.
Runtime
With a heap, everytime you heapify the k arrays, it will take O( log(k) ) time.
You will need to do this for each element in the k arrays.
So the average runtime will be O( nlog(k) ). Best-case O( n ) (just one array).
Space
Space complexity will be O( k ) or O( 1 ), depending on how you implement the heap. You could do everything in-place to reach O( 1 ) but it’s a lot of work and your interviewer may not see it as being necessary. So, just make sure you are able to talk about how you could implement it using O( 1 ) space.
We can see from the following table that the runtime and space complexity is a lot more optimal with a heap.
| Runtime | Space | |
|---|---|---|
| No heap | O( nk^2 ) worst O( n * klog(k) ) average O( n ) best |
O( log(k) ) |
| Heap | O( n*log(k) ) average O( n ) best |
O( 1 ) |
“Javascript doesn’t have a heap, sorry” 
When you are given a heap question, you might simply state that the heap isn’t a standard data structure in Javascript, and the interviewer might give you a grace pass.
But here’s something you can do to win some points.
Knowing how to implement the array-based heap will impress your interviewer.
It’s a lot easier than you may think it is.
No, you don’t need a class.
No, you don’t need dozens of lines of code.
All you need is a function that takes in an array and heapifies the array.
This requires you to understand the logic of an array-based heap. If you haven’t read it yet, read it here.
Here’s what I mean.
For Question 1, we could do something like the following:
// index starts at 1 due to the array-heap implementation
for (let i = 1; i < k; i++) {
minHeapify(array, i) // O( log(n) ) runtime
popMin(array) // O( 1 ) runtime
}
return input[1] // index starts at 1 due to the array-heap implementationYou could merge the popMin functionality inside minHeapify, but for simplicity here I won’t.
minHeapify()
Here’s my Javascript implementation of minHeapify(), which is coming from the Java implementation of percolatingDown(int n) here
function minHeapify (array, index) {
const temp = array[index]
let childIndex
for (; index * 2 < array.length; index = childIndex) {
childIndex = index * 2
// Choose the smaller of the two (left, right) children
if (childIndex != array.length - 1 && array[childIndex] > array[childIndex + 1]) {
childIndex ++
}
if (temp > array[childIndex]) {
array[index] = array[childIndex]
} else {
break
}
}
array[index] = temp
}You could use such a function for both Question 1 and Question 2.
I hope you learned something. Let me know if anything could be better explained. Happy interviewing :)